Reflection and imaging using mirrors
Light reflects from objects in two distinct ways: specular or diffuse. Well polished surfaces, particularly shiny metals, cause specular reflection. Rough surfaces lead to diffuse reflections. When light strikes an object it gets scattered. In the case of a diffuse reflection the light ray's scattering direction depends on which part of the object the ray strikes. So, a collection of parallel rays falling on a piece of paper, say, will reflect in different directions and light will reach your eye looking at the paper no matter where you stand. But when the surface is smooth so that there is no difference between different sections of the surface, then parallel rays are all reflected in the same direction and your eye will only see the rays if you stand at the right location to receive those parallel reflected rays. Even though almost all the objects that we see are illuminated by light sources, such as the sun or room light, and they themselves are diffuse reflectors, we can learn a great deal about imaging by studying specular reflections. 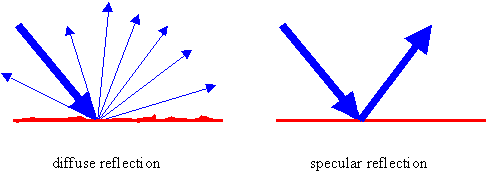 .
.
Mirrors are not only specular reflectors, they also reflect rays (laser beams) in a very well ordered way, known as the law of reflection:
Angle of incidence = Angle of reflection
This simple law is all that we need, along with the technique of ray tracing, to understand how mirrors form images and to determine the location, size, and orientation of images formed by mirrors. Mirrors differ from ordinary plate glass in that they have a thin metal coating - usually on the back surface opposite to the incident side - that is highly reflective. The metal coating can be designed to be partially reflective, so that it is partially transmissive as well, as, for example, "mirrors" on the "walls" of many stores that allow one-way vision into the store. Plane window glass reflects only about 4% of the incident light intensity at each of its two surfaces when viewing the reflection "head-on".
The simplest mirror to study is a flat mirror. Consider a point source of light located in front of a flat mirror, as shown below. In terms of wave fronts, this source sends out spherical fronts centered at the source. In terms of rays, the source sends out rays in all directions. Those rays that strike the mirror reflect according to the law of reflection. It is simple geometry to show that all of these rays reflect as if they originated from a single point behind the mirror. This apparent "source" is the virtual image of the original point source. It is called "virtual" because no light actually emanates from it, but it appears as a source of light.
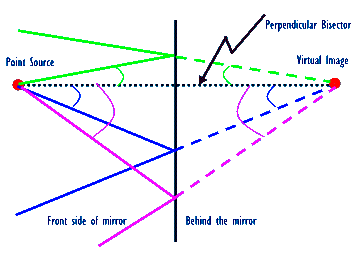
In the above diagram we see three arbitrary rays emanating from the point source that strike the mirror, each at a different angle. There are of course many other rays that are sent out from the source, but not drawn. Some of these do not get reflected from the mirror and so do not contribute to the apparent luminosity of the image. What is interesting is that all of the rays that strike the mirror are reflected so that their extensions meet at one single point. To see this, we draw a line (the black dashed line) from the point source perpendicular to the mirror. Evidently, the reflection of all rays appears to originate from a point on this line. This point is located as far behind the mirror as the source is in front of the mirror. The line that we drew is in fact the perpendicular bisector of the triangle that is formed by the incident ray and the extension of the reflected ray (virtual ray). Therefore, from the rules of simple geometry, the angle of incidence will be equal to the angle of reflection provided that the extension of the reflected ray originates from this point.
Any object (source of light) can be thought to be a collection of point sources. So, we could now determine the location, orientation, and sizes of the image of any object simply by repeated application of the above simple geometry. In the case of a straight object, say a stick or you, standing in front of the mirror, the image stands behind the mirror, an equal distance, and with the same orientation (upright). Furthermore, this image has the same size as the object as shown below:
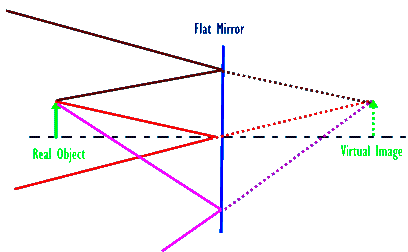
- o = object distance = distance from the object to the mirror
- i = image distance = distance from the image to the mirror
- m = magnification = - (image size)/ (object size) = - i / o
- If object is virtual, then o is assigned a negative value; if it is real, then a positive value
- If image is virtual, then i is assigned a negative value; if it is real, then a positive value
- When m is positive, the image is erect; otherwise, it is inverted.
- Real objects emanate real rays of light; virtual objects emanate extensions of real rays (i.e. virtual rays)
- Real images are where real rays come together to intersect; virtual images are where extensions of real rays meet.
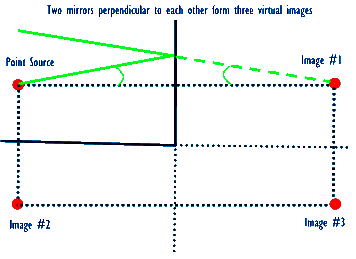
Reflection of a ball in two mirrors at right angles to each other, just as in the sketch above. Note that the lettering on the central image is correct while those on the other two are mirror-reversed. Why is that? Use the above sketch to help decipher why.
Questions on Imaging using Mirrors
Last Modified Tuesday, 23-Sep-2003 malekis@union.edu



